
Friedrich-Alexander-Universität Erlangen
Lehrstuhl für Mustererkennung
Martensstraße 3
91058 Erlangen

 |
 |
The Digital Brain Perfusion Phantom package [1] provides data and Matlab tools to create a realistic digital 4D brain phantom, in particular for reproducible evaluation of reconstruction algorithms using non-linear regularization for perfusion CT and perfusion C-arm CT. It is based on the Realistic Digital Brain Perfusion Phantom originally published by Riordan et al. [2]. Since classical digital CT phantoms usually consist of homogeneous structures and have very sparse representation in transformations like total variation or wavelets, they highly favor non-linear reconstruction algorithms. This phantom allows for a more authentic evaluation by providing a brain model based on real physiological data and avoiding sparsity by continuously varying perfusion parameters and anatomical structures using MR data.
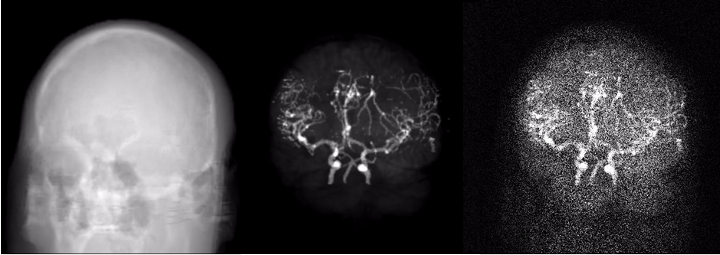
The phantom was created by segmenting brain MRI scans from a human volunteer into white and gray matter, cerebrospinal fluid (CSF), skull and arteries. White/gray matter and CSF segmentation was done from T1 weighted MRI data using the Freesurfer software [3]. The skull was segmented from a sequence of MRI scans using a dedicated algorithm [4]. Arteries were segmented from a time-of-flight acquisition by thresholding and manual post-processing. The spatial resolution corresponds to an isotropic voxel size of 1x1x1 mm^3.
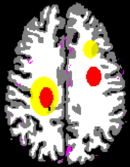
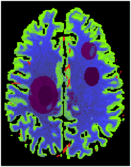
The package includes a tool to annotate areas with reduced and severely reduced perfusion inside the segmented brain and a tool to create a 4D volume consisting of time attenuation curves (TACs) corresponding to the annotated tissue areas. The TACs inside the brain tissue are simulated by convolution of an arterial input function (AIF) measured with clinical perfusion CT [2] with residual functions, which correspond to the stroke annotation. The TACs of vessel structures are simulated by the real measured AIF. Anatomic tissue structures are incorporated into the phantom by adding appropriate constants to the TACs.
To reduce the sparsity of the brain phantom, the MR data is used to vary the perfusion parameters assigned to the tissue voxels by the annotation. Therefore each tissue voxel is associated with a normalized value of its T1 weighted MR value. The MR values are normalized to interval [-1, 1] in each slice by first computing the mean and the standard deviation σ of all MR values inside the slice associated to a segmented tissue voxel. Then the mean is subtracted from the MR values and the values are limited to [-2*σ, +2*σ] by setting all values < -2*σ to -2*σ resp. all values > 2*σ to 2*σ. Finally all values are divided by 2*σ. The perfusion parameters of each tissue voxel are varied by:
PV(x) = P(x) + NMR(x) * DP(X)
PV(x) denotes the varied perfusion parameter of voxel x (CBF or MTT, CBV is defined as CBF*MTT), P(x) the default perfusion parameter of voxel x according to annotation, NMR(x) the normalized MR value and DP(x) the maximal deviation of the perfusion parameter. The HU values of the anatomic structures are varied similarly to reduce sparsity.
For an overview of computational methods to calculate perfusion parameters from reconstructed TACs see [5].
![]() Download Phantom Data and Tools (last update: Sep 09 2014)
Download Phantom Data and Tools (last update: Sep 09 2014)
[1] A. Aichert, M. Manhart, B. Navalpakkam, R. Grimm, J. Hutter, A. Maier, J. Hornegger, A. Doerfler: "A Realistic Digital Phantom for Perfusion C-Arm CT Based on MRI Data"; 2013 IEEE Nuclear Science Symposium and Medical Imaging Conference Record (NSS/MIC), Seoul, Korea, 2013.
[2] A. J. Riordan, M. Prokop, M. A. Viergever, J. W. Dankbaar, E. J. Smit, and H.W. A. M. de Jong, “Validation of CT brain perfusion methods using a realistic dynamic head phantom,” Medical Physics, vol. 38, no. 6, pp. 3212–3221, 2011.
[3] Freesurfer image analysis suite. [Online]. Available: http://surfer.nmr.mgh.harvard.edu/
[4] Navalpakkam BK, Braun H, Kuwert T, et al., Magnetic Resonance-based attenuation correction for PET/MR hybrid imaging using continuous valued attenuation maps. Invest Radiol. 2013, 48:323-332.
[5] A. Fieselmann, M. Kowarschik, A. Ganguly, J. Hornegger, and R. Fahrig, “Deconvolution-based CT and MR brain perfusion measurement: Theoretical model revisited and practical implementation details,” International Journal of Biomedical Imaging, 2011, article ID 467563.
 |